Probabilistic interpretation of AUC
Unfortunately this was not taught in any of my statistics or data analysis classes at university (wtf it so needs to be ![]() ).
So it took me some time until I learned that the AUC has a nice probabilistic meaning.
).
So it took me some time until I learned that the AUC has a nice probabilistic meaning.
What’s AUC anyway?
AUC is the area under the ROC curve. The ROC curve is the receiver operating characteristic curve. AUC is simply the area between that curve and the x-axis. So, to understand AUC we need to look at the concept of an ROC curve.
Consider:
- A dataset \(S\) : \((\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n) \in \mathbb{R}^p \times \{0, 1\}\), where
- \(\mathbf{x}_i\) is a vector of \(p\) features collected for the \(i\)th subject,
- \(y_i\) is the \(i\)th subject’s label (binary outcome variable of interest, like a disease status, class membership, or whatever binary label).
- A classification algorithm (such as logistic regression, SVM, deep neural net, or whatever you like), trained on \(S\), that assigns a score (or a “probability”) \(\hat{p}(\mathbf{x}_{\ast})\) to any new observation \(\mathbf{x}_{\ast} \in \mathbb{R}^p\) signifying the algorithm’s confidence that the label (or class) of \(\mathbf{x}_{\ast}\) is \(y_{\ast} = 1\).
Then:
- A decision threshold (or operating point) can be chosen to assign a class label (\(y_{\ast} = 0\) or \(1\)) to \(\mathbf{x}_{\ast}\) based on the value of \(\hat{p}(\mathbf{x}_{\ast})\). The chosen threshold determines the balance between how many false positives and false negatives will result from this classification.
- Plotting the true positive rate (TPR) against the false positive rate (FPR) as the operating point changes from its minimum to its maximum value yields the receiver operating characteristic (ROC) curve. Check the confusion matrix if you are not sure what TPR and FPR refer to.
- The area under the ROC curve, or AUC, is used as a measure of classifier performance.
Here is some R code for clarification:
# load some data, fit a logistic regression classifier
data(iris)
versicolor_virginica <- iris[iris$Species != "setosa", ]
logistic_reg_fit <- glm(Species ~ Sepal.Width + Sepal.Length,
data = versicolor_virginica,
family = "binomial")
y <- ifelse(versicolor_virginica$Species == "versicolor", 0, 1)
y_pred <- logistic_reg_fit$fitted.values
# get TPR and FPR at different values of the decision threshold
threshold <- seq(0, 1, length = 100)
FPR <- sapply(threshold,
function(thresh) {
sum(y_pred >= thresh & y != 1) / sum(y != 1)
})
TPR <- sapply(threshold,
function(thresh) {
sum(y_pred >= thresh & y == 1) / sum(y == 1)
})
# plot an ROC curve
plot(FPR, TPR)
lines(FPR, TPR)
A rather ugly ROC curve emerges:
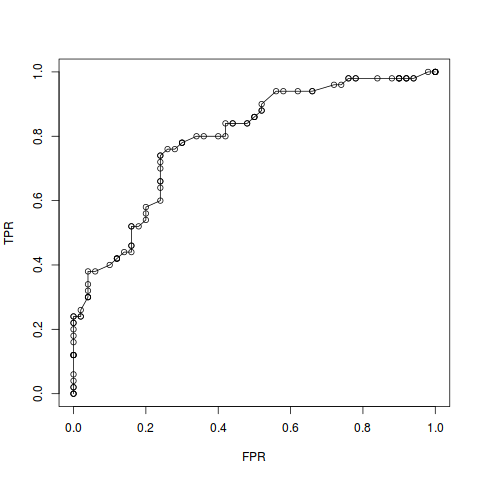
The area under the ROC curve, or AUC, seems like a nice heuristic to evaluate and compare the overall performance of classification models independent of the exact decision threshold chosen. \(\mathrm{AUC} = 1.0\) signifies perfect classification accuracy, and \(\mathrm{AUC} = 0.5\) is the accuracy of making classification decisions via coin toss (or rather a continuous coin that outputs values in \([0,1]\)…). Most classification algorithms will result in an AUC in that range. But there’s more to it.
Probabilistic interpretation
As above, assume that we are looking at a dataset where we want to distinguish data points of type 0 from those of type 1. Consider a classification algorithm that assigns to a random observation \(\mathbf{x}\in\mathbb{R}^p\) a score (or probability) \(\hat{p}(\mathbf{x}) \in [0,1]\) signifying membership in class 1. If the final classification between class 1 and class 0 is determined by a decision threshold \(t\in[0, 1]\), then the true positive rate (a.k.a. sensitivity or recall) can be written as a conditional probability
\[T(t) := P[\hat{p}(\mathbf{x}) > t \,|\, \mathbf{x}\,\text{belongs to class 1}],\]and the false positive rate (or 1 - specificity) can be written as
\[F(t) := P[\hat{p}(\mathbf{x}) > t \,|\, \mathbf{x}\,\text{does not belong to class 1}].\]For brevity of notation let’s say \(y(\mathbf{x}) = 1\) instead of “\(\mathbf{x}\) belongs to class 1”, and \(y(\mathbf{x})=0\) instead of “\(\mathbf{x}\) doesn’t belong to class 1”.
The ROC curve simply plots \(T(t)\) against \(F(t)\) while varying \(t\) from 0 to 1. Thus, if we view \(T\) as a function of \(F\), the AUC can be rewritten as follows.
\[\begin{eqnarray} \mathrm{AUC} &=& \int_0^1 T(F_0) \,\mathrm{d}F_0 \nonumber \\ &=& \int_0^1 P[\hat{p}(\mathbf{x}) > F^{-1}(F_0) \,|\, y(\mathbf{x}) = 1] \,\mathrm{d}F_0 \nonumber \\ &=& \int_1^0 P[\hat{p}(\mathbf{x}) > F^{-1}(F(t)) \,|\, y(\mathbf{x}) = 1] \cdot \frac{\partial F(t)}{\partial t} \,\mathrm{d}t \nonumber \\ &=& \int_0^1 P[\hat{p}(\mathbf{x}) > t \,|\, y(\mathbf{x}) = 1] \cdot P[\hat{p}(\mathbf{x^{\prime}}) = t \,|\, y(\mathbf{x^{\prime}}) = 0] \,\mathrm{d}t \nonumber \\ &=& \int_0^1 P[\hat{p}(\mathbf{x}) > \hat{p}(\mathbf{x^{\prime}}) \,\&\, \hat{p}(\mathbf{x^{\prime}}) = t \,|\, y(\mathbf{x}) = 1 \,\&\, y(\mathbf{x^{\prime}}) = 0] \,\mathrm{d}t \nonumber \\ &=& P[\hat{p}(\mathbf{x}) > \hat{p}(\mathbf{x^{\prime}}) \,|\, y(\mathbf{x}) = 1 \,\&\, y(\mathbf{x^{\prime}}) = 0], \nonumber \end{eqnarray}\]where we used the fact that the probability density function
\[P[\hat{p}(\mathbf{x^{\prime}}) = t \,|\, y(\mathbf{x^{\prime}}) = 0] =: f(t)\]is the derivative with respect to \(t\) of the cumulative distribution function
\[P[\hat{p}(\mathbf{x^{\prime}}) \leq t \,|\, y(\mathbf{x^{\prime}}) = 0] = 1-F(t).\]So, given a randomly chosen observation \(\mathbf{x}\) belonging to class 1, and a randomly chosen observation \(\mathbf{x^{\prime}}\) belonging to class 0, the AUC is the probability that the evaluated classification algorithm will assign a higher score to \(\mathbf{x}\) than to \(\mathbf{x^{\prime}}\), i.e., the conditional probability of \(\hat{p}(\mathbf{x}) > \hat{p}(\mathbf{x^{\prime}})\).
An alternative purely geometric proof can be found in the Scatterplot Smoothers blog.
In other words, if the classification algorithm distinguishes “positive” and “negative” examples (e.g., disease status), then
AUC is the probability of correct ranking of a random “positive”-“negative” pair.
Computing AUC
The above probabilistic interpretation suggest a simple formula to compute AUC on a finite sample:
Among all “positive”-“negative” pairs in the dataset compute the proportion of those which are ranked correctly by the evaluated classification algorithm.
Here is an inefficient implementation using results from the above logistic regression example:
s <- 0
for (i in which(y == 1)) {
for (j in which(y == 0)) {
if (y_pred[i] > y_pred[j]) {
s <- s + 1
} else if (y_pred[i] == y_pred[j]) {
s <- s + 0.5
}
}
}
s <- s / (sum(y == 1) * sum(y == 0))
s
# [1] 0.7918
The proportion of correctly ranked “positive”-“negative” pairs yields estimated \(\mathrm{AUC} = 0.7918\).
We can compare this value to the area under the ROC curve computed with the trapezoidal rule.
s <- 0
for (i in 1:(length(FPR) - 1)) {
dFPR <- abs(FPR[i+1] - FPR[i])
s <- s + 0.5 * dFPR * (TPR[i+1] + TPR[i])
}
s
# [1] 0.7922
Trapezoidal rule yields estimated \(\mathrm{AUC} = 0.7922\). The difference of \(0.0004\) can be explained by the fact that we evaluated the ROC curve at only 100 points.
Since there is a minor disagreement, let’s use some standard R package to compute AUC.
library(ROCR)
pred <- prediction(y_pred, y)
auc <- as.numeric(performance(pred, measure = "auc")@y.values)
auc
# [1] 0.7918
Same as the proportion of correctly ranked pairs! ![]()
Wilcoxon-Mann-Whitney test
By analysing the probabilistic meaning of AUC, we not only got a practically relevant interpretation of this classification performance metric, but we also obtained a simple formula to estimate the AUC of a trained classification algorithm. Well, it turns out that taking the proportion of correctly ranked “positive”-“negative” pairs as a formula to estimate the AUC is equivalent to the Wilcoxon-Mann-Whitney statistical test. This fact can also be easily demonstrated in a couple lines of R code.
y_is_1 <- which(y == 1)
y_is_0 <- which(y == 0)
n_pairs <- length(y_is_1) * length(y_is_0)
WMW_test <- wilcox.test(y_pred[y_is_1], y_pred[y_is_0])
WMW_test$statistic / n_pairs
# W
# 0.7918
Same answer!
So what? Why care about AUC anyway?
- It has a really nice probabilistic meaning!

Besides (arguably more importantly), as a measure of classification performance AUC has many advantages compared to other “single number” performance measures:
- Independence of the decision threshold.
- Invariance to prior class probabilities or class prevalence in the data.
- Can choose/change a decision threshold based on cost-benefit analysis after model training.
- Extensively used in machine learning, and in medical research – and that for good reasons, as for example explained in an excellent blog post on deep learning research in medicine by Luke Oakden-Rayner.